工程技术

数据可视化（三）基于 Graphviz 实现程序化绘图

摘要

  • 从 OmniGraffle 自动布局说起
  • 背景知识：图论
  • Graphviz 简介
  • 最佳 Graphviz 实践(一)：流程图、数据结构图、网络路径 Trace Route
  • 最佳 Graphviz 实践(二)：社会关系链分析（《红楼梦》、《权力的游戏》）
  • 最佳 Graphviz 实践(三)：可视化函数调用、算法和数据结构可视化

This article is part of an Data Visualization tutorial series. Make sure to check out my other articles as well:

前言

我之前的 数据可视化（一）思维利器 OmniGraffle 绘图指南 曾提到了力导图，在上文结尾还吐槽了一番自动布局按钮的坑。在本文中我力求将这个坑填上。

OmniGraffle 生成自动布局图形的基础是 Graphviz 引擎。Graphviz（Graph Visualization Software）是一个由AT&T实验室启动的开源工具包，能够支持基于 DOT 脚本，文件扩展名通常是 .gv 或 .dot 的描述绘制图形。DOT 是一种文本图形描述语言，将生成的图形转换成多种输出格式的命令行工具，其输出格式包括PostScript，PDF，SVG，PNG，含注解的文本等。DOT 本身非常原始，提供了一种非常简单的描述图形的方法，同时意味着可以在命令行终端使用，或者被其它编程语言调用（Graphviz 就可以作为一个库使用）。这一点非常关键，基于 Graphviz 应用开发者不必掌握布局的复杂算法，而是可以把精力放在业务方面，将最后的图对象交给绘图引擎来处理即可。

有趣的是 Graphviz(Mac 版) 和 OmniGraffle 都曾获得苹果设计奖 Apple Design Awards。

在深入掌握 Graphviz 及其相关衍生应用之前，我们有必要了解一些基础理论 —— 图论(Graph theory)。

一、背景知识：图论(Graph theory)

  • 柯尼斯堡七桥问题

东普鲁士柯尼斯堡（今日俄罗斯加里宁格勒）市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？

许多数学家都尝试去寻找这类问题的解决方案，后来发展成为了数学中的图论。图论史上第一篇重要文献是莱昂哈德·欧拉在1736年发表在圣彼得堡科学院的《柯尼斯堡的七桥》。该论文证明了柯尼斯堡七桥问题中，符合条件的走法并不存在，同时提出和解决了一笔画问题。过桥问题可以抽象简化为平面上的点与线组合，每一座桥视为一条线，桥所连接的地区视为点。从这个点出发的线有奇数条称为奇点，从这个点出发的线有偶数条称为偶点。任意一种河──桥图能否全部走一次的判定法则： 如果存在两个以上（不包括两个）奇顶点，路线不存在；且有n个奇顶点的图至少需要n/2笔画出。

1、经典适用场景

  • 路径问题（柯尼斯堡七桥问题），最小生成树问题，斯坦纳树
  • 网络流与匹配问题：最大流问题，最小割问题，最大流最小割定理，最小费用最大流问题，二分图及任意图上的最大匹配，带权二分图的最大权匹配
  • 覆盖问题：最大团、最大独立集、最小覆盖集、最小支配集

2、经典算法

  • 戴克斯特拉算法(D.A)
  • 克鲁斯卡尔算法(K.A)
  • 普里姆算法(P.A)
  • 拓扑排序算法(TSA)
  • 关键路径算法(CPA)
  • 广度优先搜索算法(BFS)
  • 深度优先搜索算法(DFS)

二、Graphviz 简明指南

1、Graphviz 布局器

总的来说，Graphviz 支持两类图：无向图（graph,用“ - - ”表示节点之间）和 有向图（digraph,用“ ->” 表示节点之间）。顶点和边都具有各自的属性，比如形状，颜色，填充模式，字体，样式等。主要的布局器如下：

  • dot: 默认布局方式，主要用于有向图(directed graphs)；
  • neato：基于 sprint model 模型，又称force-based 或者 energy minimized；
  • twopi：径向布局(radial layouts of graphs)，放射状；
  • circo：圆环布局(circular layout of graphs)；
  • fdp：无向图 (undirected graphs)；
  • sfdp: large undirected graphs patchwork 、squarified tree maps osage 、
  • dotty：一个用于可视化与修改图形的图形用户界面程序；
  • lefty：一个可以显示 DOT 图形的可编程控件，并允许用户用鼠标在图上执行操作。

2、Hello World!

1
2
$ brew install graphviz
$ dot -Tpng demo.dot -o demo.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
digraph demo{
  label="儿茶酚胺合成代谢路径";

  酪氨酸 -> L多巴 -> 多巴胺 -> 去甲肾上腺素 -> 肾上腺素;

  下丘脑 -> 多巴胺;
  交感神经元 -> 去甲肾上腺素;
  肾上腺髓质 -> 去甲肾上腺素,肾上腺素;

  酪氨酸 [label="酪氨酸",color=green];
  多巴胺 [label="多巴胺", color=red];
  肾上腺素 [label="肾上腺素", color=red];

  下丘脑 [shape=box];
  交感神经元 [shape=box];
  肾上腺髓质 [shape=box];
}

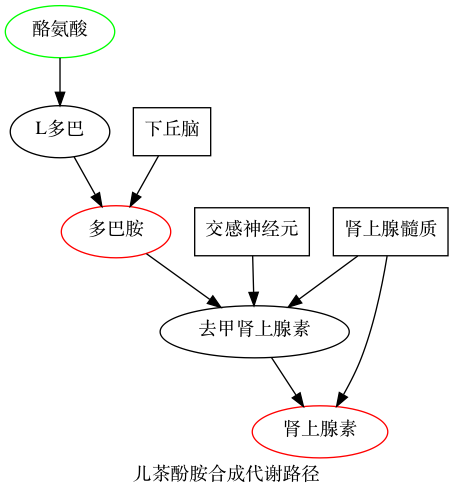
儿茶酚胺合成代谢路径-dot 布局

3、twopi 径向布局

1
2
## 缺省为 dot 布局
$ dot -Kcirco -Tpng demo.dot -o demo.png

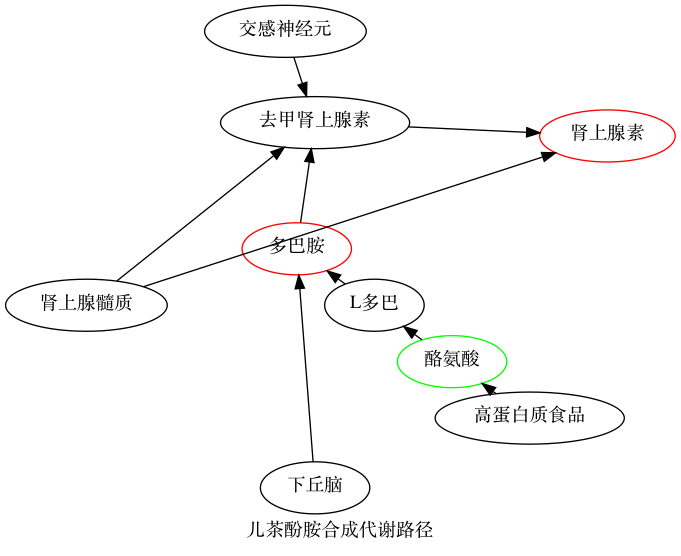
儿茶酚胺合成代谢路径-twopi 径向布局

应用场景

1、软件工程领域

软件工程领域的主要应用：

  • 系统分析统一建模，时序图、用例图、类图、活动图、组件图、状态图、对象图等。
  • 可视化函数调用、包依赖关系分析
  • 可视化数据结构

基于 Graphviz 的开源项目 PlantUML 支持快速绘制各类 UML 图形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
@startuml
scale 600 width

[*] -> State1
State1 --> State2 : Succeeded
State1 --> [*] : Aborted
State2 --> State3 : Succeeded
State2 --> [*] : Aborted
state State3 {
  state "Accumulate Enough Data\nLong State Name" as long1
  long1 : Just a test
  [*] --> long1
  long1 --> long1 : New Data
  long1 --> ProcessData : Enough Data
}
State3 --> State3 : Failed
State3 --> [*] : Succeeded / Save Result
State3 --> [*] : Aborted

@enduml

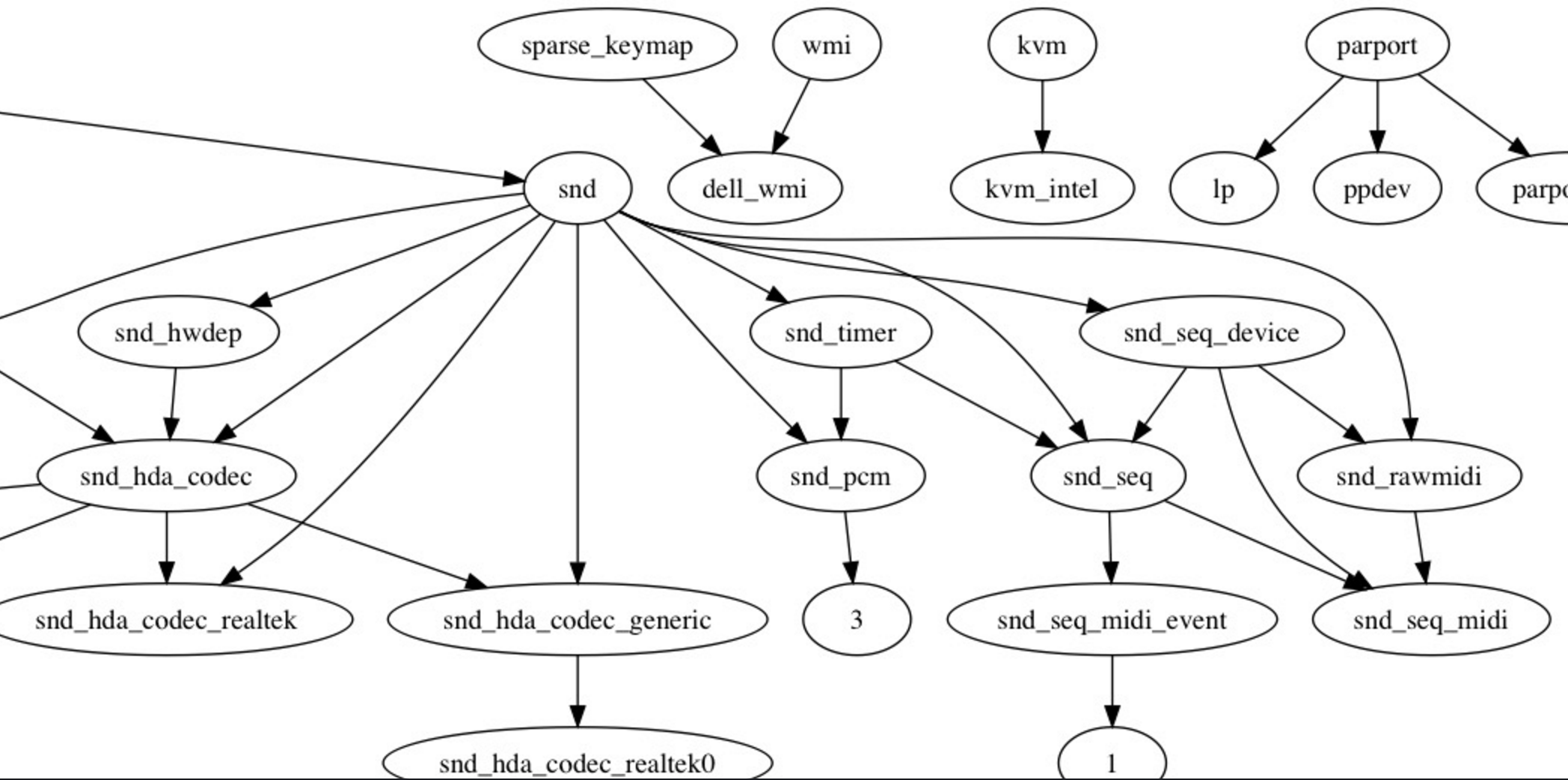
Linux 内核内部结构非常复杂，从概念上就由五个主要的子系统构成：进程调度器模块、内存管理模块、虚拟文件系统、网络接口模块和进程间通信模块。这些模块之间通过函数调用和共享数据结构进行数据交互，在涉及内核版本、应用程序升级等场景中，弄清楚模块之间的依赖关系非常重要。

lsmod 命令用于显示已经加载到内核中的模块的状态信息，Used by表示依赖的内容。通过 lsmod 命令获取依赖信息之后，简单处理就可以转化为图形，而且图形生成的全过程可以由程序固化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
$ lsmod
Module          Used by
vboxdrv         vboxnetadp,vboxnetflt,vboxpci
nf_reject_ipv4  ipt_REJECT
ebtables        ebtable_filter
ip6_tables      ip6table_filter
ip6_udp_tunnel  vxlan
udp_tunnel      vxlan
xor             btrfs
raid6_pq        btrfs
nf_nat_masquerade_ipv4       ipt_MASQUERADE
xfrm_algo        xfrm_user
nf_defrag_ipv4        nf_conntrack_ipv4

......

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
digraph kernel{
        vboxdrv->vboxnetadp,vboxnetflt,vboxpci;
        nf_reject_ipv4->ipt_REJECT;
        ebtables->ebtable_filter;
        ip6_tables->ip6table_filter;
        ip6_udp_tunnel->vxlan;
        udp_tunnel->vxlan;
        xor->btrfs;
        raid6_pq->btrfs;
        nf_nat_masquerade_ipv4->ipt_MASQUERADE;
        xfrm_algo->xfrm_user;
        nf_defrag_ipv4->nf_conntrack_ipv4;

        ......
}

软件包依赖案例-Linux Kernel 3

2、通信工程领域

  • nwdiag 是一个基于 Python 的、支持 Dot 脚本生成网络图的库
  • 结合 GIS 信息追踪网络路由

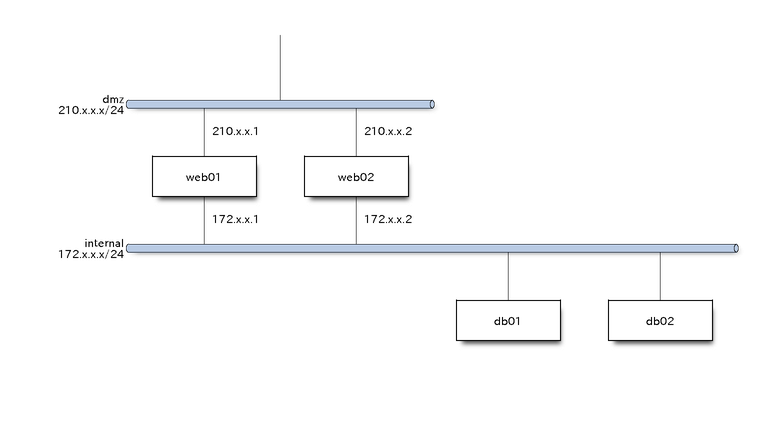
网络拓扑图

1
2
3
pip install nwdiag
nwdiag simple.diag
nwdiag -Tsvg simple.diag
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
nwdiag {
  network dmz {
      address = "210.x.x.x/24"

      web01 [address = "210.x.x.1"];
      web02 [address = "210.x.x.2"];
  }
  network internal {
      address = "172.x.x.x/24";

      web01 [address = "172.x.x.1"];
      web02 [address = "172.x.x.2"];
      db01;
      db02;
  }
}

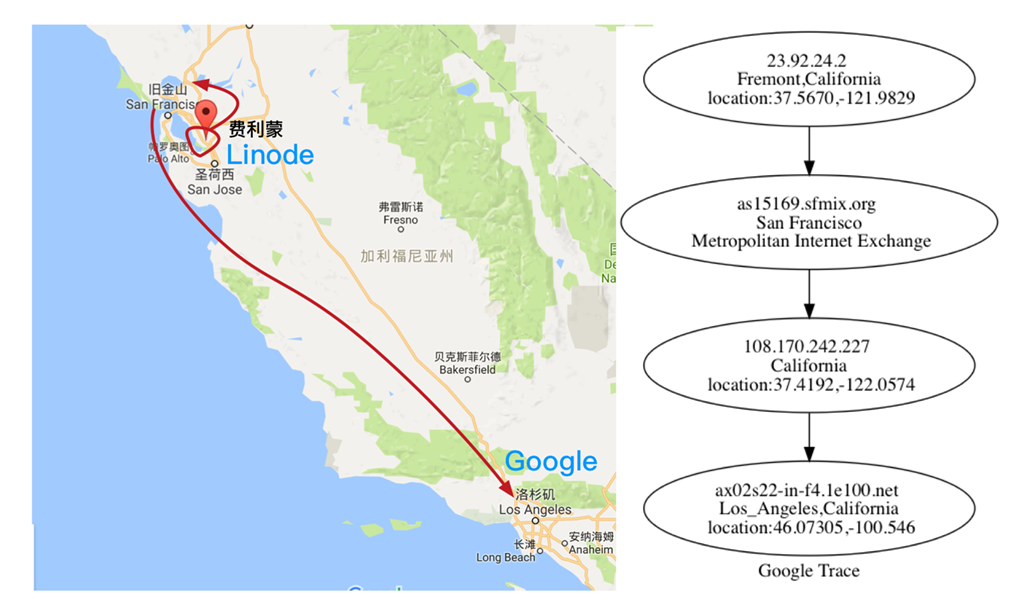
traceroute 案例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[root@li1437-101 ~]# traceroute www.google.com
traceroute to www.google.com (216.58.216.36), 30 hops max, 60 byte packets
 1  23.92.24.2 (23.92.24.2)  0.704 ms  0.736 ms 23.92.24.3 (23.92.24.3)  0.575 ms
 2  173.230.159.16 (173.230.159.16)  0.910 ms 173.230.159.14 (173.230.159.14)  2.265 ms
 		173.230.159.0 (173.230.159.0)  0.731 ms
 3  as15169.sfmix.org (206.197.187.50)  4.039 ms eqixsj-google-gige.google.com (206.223.116.21)  0.718 ms
 		as15169.sfmix.org (206.197.187.50)  3.944 ms
 4  108.170.242.227 (108.170.242.227)  4.902 ms
 		108.170.242.226 (108.170.242.226)  3.003 ms
 		108.170.243.2 (108.170.243.2)  3.064 ms
 5  216.239.47.37 (216.239.47.37)  4.836 ms 64.233.174.91 (64.233.174.91)  1.476 ms  1.447 ms
 6  216.239.54.22 (216.239.54.22)  12.464 ms  29.292 ms 64.233.174.204 (64.233.174.204)  9.032 ms
 7  209.85.245.172 (209.85.245.172)  10.633 ms
    108.170.230.130 (108.170.230.130)  20.010 ms
 		108.170.230.124 (108.170.230.124)  8.988 ms
10  lax02s22-in-f4.1e100.net (216.58.216.36)  10.358 ms  10.383 ms  10.301 ms
1
2
3
4
5
6
7
8
digraph {
    label="Google Trace Sample";
    "23.92.24.2" [label="23.92.24.2 \n Fremont,California \n location:37.5670,-121.9829"] ;
    as15169 [label="as15169.sfmix.org \n San Francisco \n Metropolitan Internet Exchange"];
    "108.170.242.227" [label="108.170.242.227 \n California \n location:37.4192,-122.0574"];
    lax02s22 [label="ax02s22-in-f4.1e100.net \n Los_Angeles,California \n location:46.07305,-100.546"];
    "23.92.24.2" -> as15169 -> "108.170.242.227"  -> lax02s22;
}

3、社会工程领域

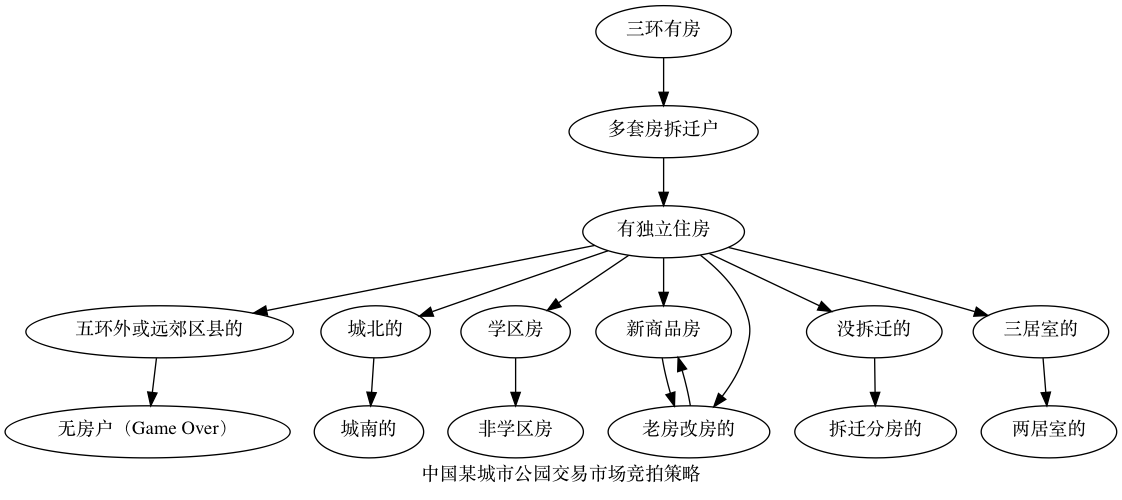
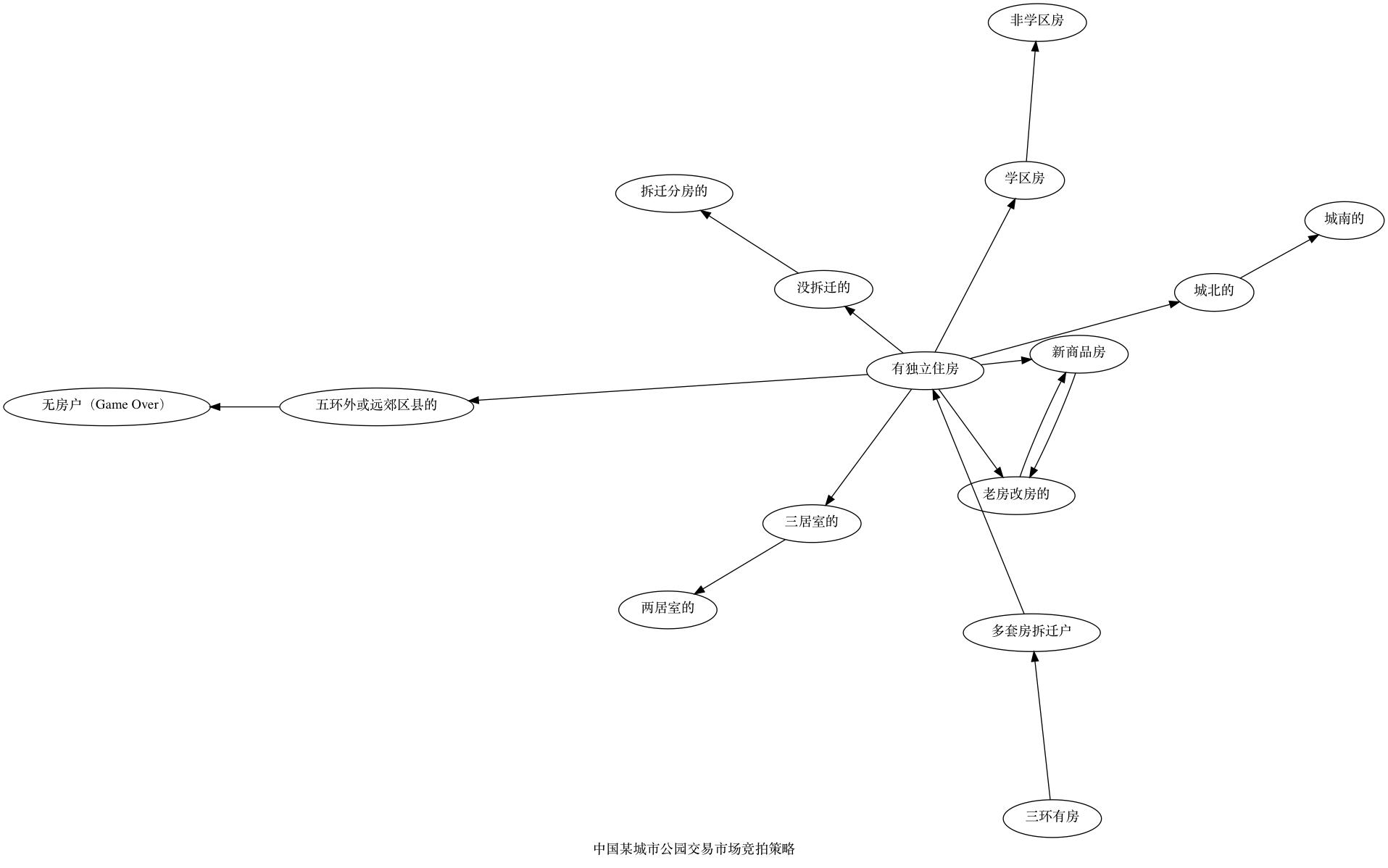
  • 决策树(Decision Tree)：人群鄙视链
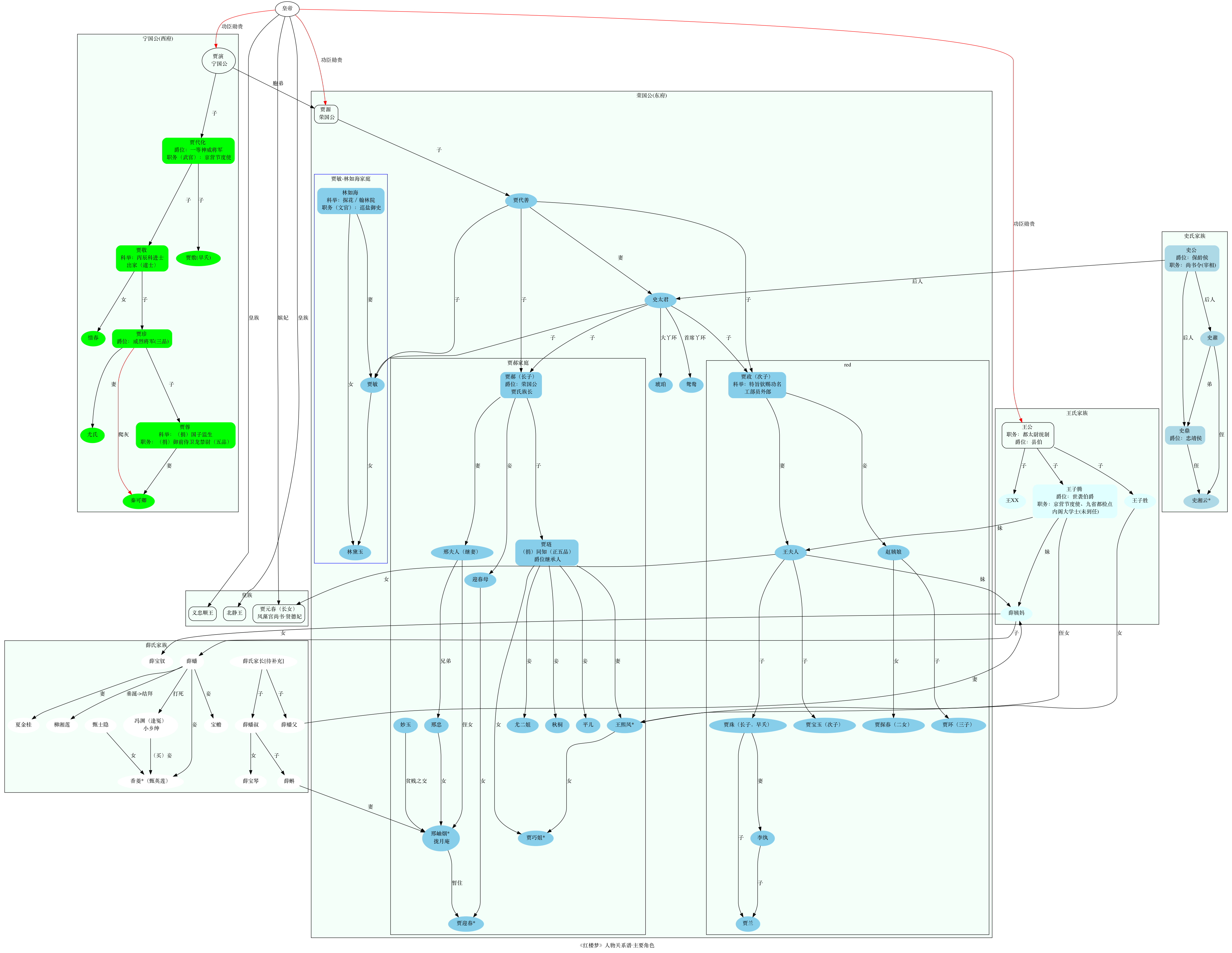
  • 复杂人物关系链分析（《红楼梦》、《权力的游戏》）

鄙视链案例-婚姻市场中的房市-dot

鄙视链案例-婚姻市场中的房市-circo-圆环布局

注意: 如果需要使用分组（Group）特性，子图的名称必须以“cluster”开头，否则无法识别

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
digraph family {
  label ="《红楼梦》人物关系谱·主要角色";

  subgraph cluster_皇族{
      label ="皇族";
      bgcolor="mintcream";
      node [ color="lightyellow", style="filled"];

      北静王 [label = "北静王",shape="Mrecord"];
      义忠顺王 [label = "义忠顺王",shape="Mrecord"];

      贾元春 [label = "贾元春（长女）\n 凤藻宫尚书·贤德妃",shape="Mrecord"];
  }

  subgraph cluster_宁国公{
      label ="宁国公(西府)";
      bgcolor="mintcream";
      node [ color="green", style="filled"];

      贾演 [label = "贾演 \n 宁国公"];

      贾代化[label = "贾代化 \n 爵位：一等神威将军 \n 职务（武官）：京营节度使",shape="Mrecord"];
      贾演 -> 贾代化[label = "子"];

    }

}

《红楼梦》人物关系谱·主要角色

Resources

扩展阅读：数据可视化

参考文献

推荐文章