工程技术

读书笔记|数学之美（Beauty Of Mathmetics）

摘要

  • 作者：吴军
  • 起源：Google中国的官方博客–谷歌黑板报连载的系列博客
  • 主题：自然语言处理、科技史

数学的魅力就在于将复杂的问题复杂化

人类信息交流的发展贯穿了人类的进化和文明的全过程。而自然语言是人类交流信息的工具，语言和通信的联系是天然的。通信的本质就是一个解编码和传输的过程。（p49）

《数学之美》 Topic

  • 自然语言识别与概率论：第 3、5、24 章
  • 信息论：第 6 章

第一章 文字和语言 vs 数字和信息

故事：罗赛塔石牌、犹太人抄圣经（校验）、口语和文言文（信道压缩）

  • 通信的原理和信息传播的模型
  • （信源）编码和最短编码
  • 解码的规则，语法
  • 聚类
  • 校验位
  • 双语对照文本，语料库和机器翻译
  • 多义性和利用上下文消除歧义性

第二章 自然语言处理——从规则到统计

Tips:

自然语言发展阶段

  • 20世纪50-70年代：基于规则的方法，电脑模拟人脑理解语法、文法，收效甚微
  • 20世纪70年代以后：基于数学模型和统计的方法。例如翻译，计算机不需要像人类一样理解两种语言。

人物

长达15年的对峙时期

两派人马各自召开自己的会议，持续争议。

基于统计方法的发展

  • 上世纪70年代：基于统计的方法的核心模型是通信系统加隐含马尔可夫模型。
    输入和输出都是一维的符号序列，保持原有的次序。最早的语音识别、词性分析取得成果；句法分析中输入的是一维的句子，输出的是二维的分析树；机器翻译中，输出的句子次序会有很大变化，效果不佳。

  • 1998年，彼得·布朗(Peter Brown) | IBM 等提出了基于统计的机器翻译方法效果很差，模型、数据不足。
    （文艺复兴技术公司）

  • 基于有向图的统计模型解决复杂的句法分析。

  • 20世纪90年代末期：通过统计得到的句法规则甚至比语言学家总结的更有说服力。

  • 2005年，Google 基于统计方法的翻译系统全面超过基于规则方法的 SysTran 翻译系统

科学史的教训：等待老科学家退休

基于统计的方法代替传统的方法，需要等原有的一批语言学家退休。“老的科学家” 或者 “老科学的家” （钱钟书《围城》），后一种年纪不算老，但是已经落伍，大家必须耐心等待他们退休让出位子。毕竟，不是所有人都乐意改变自己的观点，无论对错。 …… 因此，我常想，我自己一定要在还不太糊涂和固执时就退休（p25）

第三章 统计语言模型

计算机处理自然语言的基本问题：为自然语言这种上下文相关的特性建立数学模型，即 统计语言模型（Statistical Language Model）

贾里尼克：一个句子是否合理，就看看它的可能性大小如何。可能性用概率来衡量。

P(S) = P(W1 ,W2, … , Wn)
=P(W1)·P(W2|W1) ·P(W3|W1,W2) ··· P(Wn | W1,W2, … , Wn-1)

S 表示某一个有意义的句子，由一连串特定顺序排列的词W1,W2, ··· , Wn 组成，n 是句子的长度。句子越长，条件概率 P(Wn | W1,W2, … , Wn-1) 的可能性越多，无法估算。

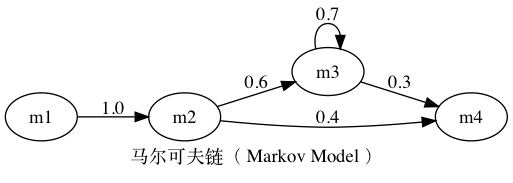
19 世纪到 20 世纪初，马尔可夫（Andrey Markov）提出假设，任意一个词 Wi 出现的概率只同它前面的词 Wi-1有关，偷懒但颇为有效的方法。【符合这个假设的随机过程则称为马尔科夫过程，也称为马尔可夫链。】二元模型（ Bigram Model ）对应的公式如下：

P(S) = P(W1 ,W2, … , Wn)
=P(W1)·P(W2|W1) ·P(W3|W2) ··· P(Wi | Wi-1) ··· P(Wn | Wn-1)

语料库（ Corpus ）: 大量机读样本
相对频度
根据 大数定理（ Law of Large Numbers ），只要统计量足够，相对频度就等于概率
推导过程省略（P30）

延伸阅读：统计语言模型的工程诀窍

  • 2.1 高阶语言模型
    很少有人能使用四元以上的模型，Google 的罗塞塔翻译系统和语言搜索引擎使用四元模型，该模型存储于 500 台 以上的 Google 服务器中。

马尔可夫假设的局限性：自然语言中上下文相关性跨度可能非常大，需采用其他一些 长程的依赖性（ Long Distance Dependency ） 来解决。

  • 2.2 模型的训练、零概率问题和平滑方法

  • 古德·图灵估计（ Good-Turing Estimate）

一种概率估计方法：1953年，古德（ I. J. Good）、图灵（ Alan Turing ）提出，在统计中相信可靠的统计数据，而对不可信的统计数据打折扣，同时将折扣出来的那一小部分概率给予未看见的事件（ Unseen Events ）。

如果训练语料与模型应用的领域相脱节，那么模型的效果通常要大打折扣。例如腾讯搜索部门的语言模型，最早使用《人民日报》的语料训练（干净、无噪音），实际效果不佳，之后使用网页的数据，尽管有很多噪音但是训练数据与应用一致，搜索质量反而好。

第四章 谈谈中文分词

  • 早期的分词：《说文解字》和《论语》注解，目的都是为了以一家的理解消除歧义性
  • 分词准确率：不是越高越好，而要看所谓正确的人工分词的数据是如何得来的。我们甚至只能讲某个分词器和另一个分词器相比，与人工分词结果的吻合度稍微高一点而已。目前采用统计语言模型，（选择哪种分词器）效果都差不到哪里去。

第五章 隐含马尔可夫模型

计划：201706
通读：201709

人类信息交流的发展贯穿了人类的进化和文明的全过程。而自然语言是人类交流信息的工具，语言和通信的联系是天然的。通信的本质就是一个解编码和传输的过程。但是自然语言处理早期的努力都集中在语法、语义和知识表述上，离通信的原理越来越远，而这样答案也就越来越远。当自然语言处理的问题回归到通信系统中的解码问题时，很多难题都迎刃而解了。（p49）

  • 雅格布森（ Roman Jakobson）提出的通信六个要素
1
2
3
4
5
6
7
8
9
10
11
digraph communicate{
  label="雅格布森提出的通信六个要素";

  信息和上下文[label = "信息和上下文(发送者)"];
  传递的信息[label = "传递的信息(信道)"];
  接收的信息[label = "接收的信息(接收者)"];

  信息和上下文 -> 传递的信息[label = "编码(S1,S2,S3,···)"];
  传递的信息 -> 接收的信息[label = "解码(O1,O2,O3,···)"];

}
  • 马尔可夫链：符合这个马尔可夫假设的随机过程则称为马尔科夫过程。
1
2
3
4
5
6
7
8
9
digraph markov{
  label = " 马尔可夫模型（ Markov Model ）";
  rankdir = LR;
  m1->m2[label = "1.0"];
  m2->m3[label = "0.6"];
  m3->m4[label = "0.3"];
  m2->m4[label = "0.4"];
  m3->m3[label = "0.7"];
}

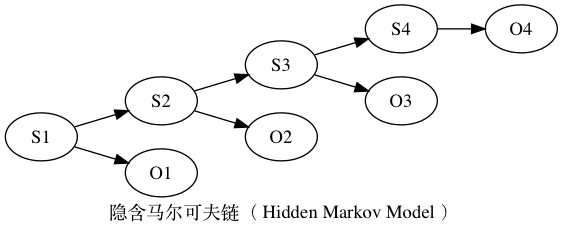
  • 隐含马尔可夫模型（ Hidden Markov Model ）
    最早由20世纪六七十年代，美国数学家鲍姆（ Leonard E. Baum ） 发表的一系列论文中提出。隐含马尔可夫模型是马尔可夫链的一个扩展，即任一时刻 t 的状态 St 是不可见的。但是，在每个时刻 t 会输出一个富豪 Ot ，而且 Ot 和 St 相关且仅和 St 相关。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
digraph hiddenmarkov{
  label = " 隐含马尔可夫模型（ Hidden Markov Model ）";
  rankdir = LR;

  S1->S2[label = ""];
  S1->O1[label = ""];

  S2->S3[label = ""];
  S2->O2[label = ""];

  S3->S4[label = ""];
  S3->O3[label = ""];

  S4->O4[label = ""];
}

  • 隐马尔可夫模型的应用
    隐含马尔可夫模型成功的应用最早是语音识别（Sphinx——大词汇量连续语音识别系统）。根据应用的不同而有不同的名称,例如语音识别中的声学模型（ Acoustic Model ），机器翻译中的翻译模型（ Translation Model ）等。

延伸阅读隐含马尔可夫模型的训练

  • 知识背景：概率论
  • 围绕隐含马尔可夫模型的基本问题
    1. 给定一个模型，如何计算某个特定输出序列的概率；
      Forward-Backward 算法
      参考书 Frederick Jelinek《Statistical Methods for Speech Recognition(Language, Speech, and Communication)》
    2. 给定一个模型和某个特定的输出序列，如何找到最可能产生这个输出的状态序列
      解码算法：维特比算法
    3. 给定足够量的观测数据，如何估计隐含马尔可夫模型的参数。
      绚练算法：鲍姆-韦尔奇算法（Baum-Welch Algorithm）

第六章 信息的度量和作用

  • 信息熵
    要搞清楚意见非常非常不确定的事，或是我们一无所知的事情，就需要了解大量的信息。
    相反，如果我们对某件事已经有了较多的了解，那么不需要太多的信息就能把它搞清楚。
    所以，从这个角度来看，可以认为，信息量就等于不确定性的多少。

  • 信息的作用
    在英语里，信息和情报是同一个词（ Information ），而我们知道情报的作用就是排除不确定性。

  • 案例：斯大林、日军南下战略情报

如果没有信息，任何公式或者数字的游戏都无法排除不确定性。这个朴素的结论非常重要，但是在研究工作中经常被一些半瓶子醋的专家忽视，希望做这方面工作的读者谨记。

几乎所有的自然语言处理、信息与信号处理的应用都是一个消除不确定性的过程。

延伸阅读：信息论在信息处理中的应用

  • 信息熵
  • 冗余度 ( Redundancy )
  • 互信息 ( Mutual Information )，量化地度量相关性
  • 相对熵 ( Relative Entropy 或 Kullback-Leibler Divergence )

信息论参考文献

  • 《A Mathematic Theory of Communication》(“通信的数学原理”)，香农（ Claude Shannon ）,1948
  • 《Elements of Information Theory》(“信息论基础”)，托马斯·科弗（ Thomas Cover ）

第七章 贾里尼克和现代语言处理

第八章 简单之美——布尔代数和搜索引擎的索引

第九章 图论和网络爬虫

计划：201706
通读：20170927

  • 交通路径规划
  • 深度优先搜索（ Depth-First Search , DFS）
  • 广度优先搜索（ Breadth-First Search , BFS）
  • 网络爬虫 ( Web Crawlers ) ：超链接 ( Hyperlinks )

延伸阅读：图论的亮点补充说明

  1. 欧拉七桥问题的证明
  2. 构建网络爬虫的工程要点：
    1）搜索引擎的调度（BFS）
    2）页面分析和 URL 的提取
    3）记录哪些网页已经下载（ URL 表）

很多数学方法就是这样，看上去没有什么实际用途，但是随着时间的推移会一下子派上大用场。这恐怕是世界上还有很多人毕生研究数学的原因。

第十章 PageRank——Google的民主表决式网页排名技术

第十一章 如何确定网页和查询的相关性

第十二章 地图和本地搜索的最基本技术——有限状态机和动态规划

第十三章 Google AK-47的设计者——阿米特-辛格博士

第十四章 余弦定理和新闻的分类

第十五章 矩阵运算和文本处理中的两个分类问题

第十六章 信息指纹及其应用

第十七章 由电视剧《暗算》所想到的——谈谈密码学的数据原理

计划：201706

第十八章 闪光的不一定是金子——谈谈搜索引擎反作弊问题

第十九章 谈谈数学模型的重要性

第二十章 不要把鸡蛋放在一个篮子里——谈谈最大熵模型

第二十一章 拼音输入法的数学模型

第二十二章 自然语言处理的教父马库斯和他的优秀弟子们

第二十三章 布隆过滤器

第二十四章 马尔可夫链的扩展——贝叶斯网络

计划：201706
通读：20170925

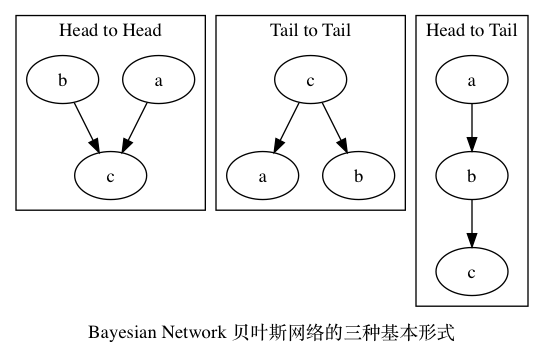
贝叶斯网络（Bayesian network） 是一种概率图型模型。

一般而言，贝叶斯网络中的节点表示随机变量，连接两个节点的箭头代表此两个随机变量是具有因果关系的；而两个节点间若没有箭头相互连接一起，表明他们之间没有直接的因果关系（注：并不表明A不会通过其他状态间接地影响状态B）。所有这些（因果）关系，都可以有一个量化的可信度（Belief）,用一个概率描述。也就是说，贝叶斯网络的弧上可以有附加的权重。因此，贝叶斯网络也被称作 信念网络（Belief Networks） 或者 有向无环图模型（directed acyclic graphical model） 。

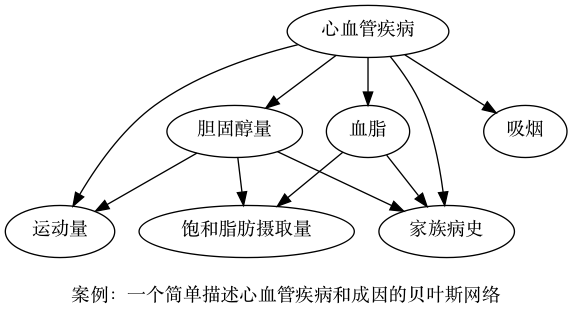
案例：描述心血管疾病和成因

一个简单的贝叶斯网络案例，描述心血管疾病和成因。

1
2
3
4
5
6
7
8
9
10
11
12
13
digraph diseaseCVD{
  label="\n 案例：一个描述心血管疾病和成因的贝叶斯网络 \n";
  心血管疾病->胆固醇量;
  心血管疾病->血脂;
  心血管疾病->吸烟;
  心血管疾病->运动量;
  心血管疾病->家族病史;
  胆固醇量->运动量;
  胆固醇量->饱和脂肪摄取量;
  胆固醇量->家族病史;
  血脂->饱和脂肪摄取量;
  血脂->家族病史;
}

上面的例子进一步简化之后，假定只有三个状态 “心血管疾病”，“高血脂”和“家族病史”。假定每个状态只有“有”、“无”两种，并且给出组合状态的条件概率。

1
2
3
4
5
6
digraph SimpleDiseaseCVD{
  label="\n 案例：心血管疾病和成因的贝叶斯网络（简化） \n";
  心血管疾病->高血脂;
  心血管疾病->家族病史;
  高血脂->家族病史;
}
心血管疾病 家族病史、高血脂 有 无
有 有 0.9 0.1
有 无 0.4 0.6
有 有 0.4 0.6
有 无 0.1 0.9
高血脂 家族病史 有 无
有 有 0.4 0.6
有 无 0.1 0.9

联合概率分布（贝叶斯公式）：

P(家族病史，高血脂，心血管疾病) = P（家族病史|高血脂，心血管疾病）x P（高血脂|家族病史）x P（家族病史）

例如，计算心血管疾病有多大概率是由家族病史引起的。

P(家族病史|有心脏病) = P（有家族病史，有心脏病）/ P（有心脏病）

其中：

P(有家族病史，有心脏病) = P（有家族病史，有心脏病，无高血脂）+ P（有家族病史，有心脏病，有高血脂）

P(有心脏病) = P（有家族病史，有心脏病，无高血脂）+ P（有家族病史，有心脏病，有高血脂）+ P（无家族病史，有心脏病，无高血脂）+ P（无家族病史，有心脏病，有高血脂）

P(有家族病史，有心脏病) = 0.18 x 0.4 + 0.12 x 0.4
= 0.12

P(有心脏病) = 0.12 + 0.08x0.4 + 0.72x0.1
= 0.12 + 0.144
= 0.264

第二十五章 条件随即场和句法分析

第二十六章 维特比和他的维特比算法

第二十七章 再谈文本自动分类问题——期望最大化算法

第二十八章 逻辑回归和搜索广告

第二十九章 各个击破算法和Google云计算的基础

第三十章 逻辑回归和搜索广告

扩展阅读

参考文献

推荐文章